Solved Examples on Piecewise Functions

$ x = -1 \\[3ex] First\:\: piece \\[3ex] f(x) = |x| + 1 \\[3ex] f(-1) = |-1| + 1 \\[3ex] f(-1) = 1 + 1 \\[3ex] f(-1) = 2 $

To find the y-intercept, set x to zero and solve for y
x is zero in the domain of the first piece because 0 < 3
So, only the first piece: 6x − 5 should be used to find the y-intercept.

$ Total\;\;time = x\;minutes \\[3ex] \underline{3rd\;\;Basic\;\;Plan} \\[3ex] charge = \$149.99 \\[3ex] time = 1400\;minutes \\[3ex] \underline{Extra} \\[3ex] charge\;\;per\;\;minute = \$0.20 \\[3ex] time = x - 1400\;minutes \\[3ex] charge = 0.20(x - 1400) \\[3ex] \underline{Total\;\;charge\;\;before\;\;taxes} \\[3ex] Total\;\;charge = Basic\;\;charge + Extra\;\;charge \\[3ex] = 149.99 + 0.20(x - 1400) $

$ 4\;\;falls\;\;in\;\;the\;\;second\;\;piece \\[3ex] f(x) = -\dfrac{1}{2}x - 3 \\[5ex] f(4) = -\dfrac{1}{2}(4) - 3 \\[5ex] f(4) = -1(2) - 3 \\[3ex] f(4) = -2 - 3 \\[3ex] f(4) = -5 $

$ x \gt 1500 \\[3ex] \underline{New\:\: rate} \\[3ex] Monthly\:\: service\:\: charge = 11.00 \\[3ex] First\:\: 1500 \\[3ex] 6.7¢/kWh = \$0.067/kWh \\[3ex] Energy-use\:\: charge = 1500 @ 6.7¢/kWh = 1500(0.067) \\[3ex] Over\:\: 1,500 \\[3ex] Remaining:\:\: (x - 1500) \\[3ex] 6.2¢/kWh = \$0.062/kWh \\[3ex] Energy-use\:\: charge = (x - 1500) @ 6.2¢/kWh = (x - 1500)(0.062) \\[3ex] Total\:\: charge = 11 + 1500(0.067) + (x - 1500)(0.062) \\[3ex] Total\:\: charge = 11 + 0.067(1500) + 0.062(x - 1500) \\[3ex] $ Please stop here because the ACT is a timed exam. The answer is Option $K$
But, I want to simplify completely.

$ Total\:\: charge = 11 + 100.5 + 0.062x - 93 \\[3ex] Total\:\: charge = 0.062x + 18.5 $

$ \underline{First\;\;Piece} \\[3ex] Maximum\;\;amount = 0.4(200) = 80 \\[3ex] \underline{Second\;\;Piece} \\[3ex] Maximum\;\;amount = 0.5(300) = 150 \\[3ex] \$80 + \$150 = \$230 \\[3ex] 230 \lt 350 \\[3ex] So,;\;move\;\;to\;\;the\;\;third\;\;piece \\[3ex] \underline{Third\;\;Piece} \\[3ex] Let\;\;x = number\;\;of\;\;candy\;\;bars \\[3ex] \implies \\[3ex] 230 + 0.6(x - 500) = 350 \\[3ex] 230 + 0.6x - 300 = 350 \\[3ex] 0.6x - 70 = 350 \\[3ex] 0.6x = 350 + 70 \\[3ex] 0.6x = 420 \\[3ex] x = \dfrac{420}{0.6} \\[5ex] x = 700 \\[3ex] $ The squad must sell 700 candy bars to reach their goal of raising $350.00

$ \underline{Check} \\[3ex] \underline{Third\;\;Piece} \\[3ex] Maximum\;\;amount = 0.6(700 - 500) = 0.6(200) = 120 \\[3ex] \underline{All\;\;Pieces} \\[3ex] Maximum\;\;amount = 230 + 120 = \$350 $

(a.)
Delivery charge: 30 therms falls in the 1st piece
Natural gas cost: 30 therms falls in the 1st piece

$ Monthly\;\;service\;\;charge = \$21.45 \\[3ex] Delivery\;\;charge: = 0.94317(30) = \$28.2951 \\[3ex] Natural\;\;gas\;\;cost: = 0.3709(30) = \$11.127 \\[3ex] C(x) = 21.45 + 28.2951 + 11.127 = 60.8721 \\[3ex] C(x) \approx \$60.87 \\[3ex] $ (b.)
Delivery charge and Natural gas cost: 200 therms falls in the 2nd piece
However:
But, 40 therms from it goes to the 1st piece (maximum limit for the 1st piece)
Remaining 160 (200 − 40) therms goes to the 2nd piece

$ Monthly\;\;service\;\;charge = \$21.45 \\[3ex] Delivery\;\;charge: = 0.94317(40) + 0(160) = 37.7268 + 0 = \$37.7268 \\[3ex] Natural\;\;gas\;\;cost: = 0.3709(40) + 0.5138(160) = 14.836 + 82.208 = \$97.044 \\[3ex] C(x) = 21.45 + 37.7268 + 97.044 = 156.2208 \\[3ex] C(x) \approx \$156.22 \\[3ex] $ (c.) The monthly cost (monthly service charge and delivery charge and natural gas cost): C depends on the amount of natural gas used: x
The monthly cost is the dependent variable
The natural gas usage is the independent variable
We write that: C = f(x) or preferably as: C(x)

To write the piecewise function, begin with the domains
The domain for the first piece should be natural gas usage from 0 to 40 therms: 0 ≤ x ≤ 40
The domain for the second piece should be any natural gas usage over 40: x ≥ 40

Next: we write the function for each piece.
First Piece: In the first example, replace 30 with x
Second Piece: In the second example, replace 160 (200 − 40) with x − 40

$ First\;\;Piece \\[3ex] C(x) = 21.45 + 0.94317(x) + 0.3709(x) \\[3ex] C(x) = 21.45 + 1.31407x \\[3ex] Second\;\;Piece \\[3ex] C(x) = 21.45 + 0.94317(40) + 0(x - 40) + 0.3709(40) + 0.5138(x - 40) \\[3ex] C(x) = 21.45 + 37.7268 + 0 + 14.836 + 0.5138x - 20.552 \\[3ex] C(x) = 53.4608 + 0.5138x \\[3ex] $ The Piecewise Function is:

$ C(x) = \begin{cases} 21.45 + 1.31407x; \hspace{3em} 0 \le x \le 40 \\[3ex] 53.4608 + 0.5138x; \hspace{2.5em} x \gt 40 \end{cases} $

$ -1 \lt 0 ...2nd\;\;Piece \\[3ex] P(x) = -x^5 + x^4 + 36x - 36 \\[3ex] P(-1) = -(-1)^5 + (-1)^4 + 36(-1) - 36 \\[3ex] P(-1) = -(-1) + 1 - 36 - 36 \\[3ex] P(-1) = 1 + 1 - 36 - 36 \\[3ex] P(-1) = -70 $

Let:
m = the mileage (number of miles)
C(m) = cost per mile (mileage rate)

$ \underline{1st\;\;Piece} \\[3ex] Domain:\;\; 0 \lt m \le 100 \\[3ex] Function:\;\; C(m) = 0.55m \\[5ex] \underline{2nd\;\;Piece} \\[3ex] Domain:\;\; 100 \lt m \le 400 \\[3ex] Function:\;\; C(m) = 0.55(100) + 0.4(m - 100) \\[3ex] C(m) = 55 + 0.4m - 40 \\[3ex] C(m) = 0.4m + 15 \\[5ex] \underline{3rd\;\;Piece} \\[3ex] Domain:\;\; 400 \lt m \le 800 \\[3ex] Function:\;\; C(m) = 0.55(100) + 0.4(300) + 0.3(m - 400) \\[3ex] C(m) = 55 + 120 + 0.3m - 120 \\[3ex] C(m) = 0.3m + 55 \\[5ex] \underline{4th\;\;Piece} \\[3ex] Domain:\;\; 800 \lt m \le 960 \\[3ex] Function:\;\; C(m) = 0.55(100) + 0.4(300) + 0.3(400) + 0(m - 800) \\[3ex] C(m) = 55 + 120 + 120 + 0 \\[3ex] C(m) =\$295 \\[5ex] $ The Piecewise Function is:

$ C(m) = \begin{cases} 0.55m; \hspace{4.5em} 0 \lt m \le 100 \\[3ex] 0.4m + 15; \hspace{2.5em} 100 \lt m \le 400 \\[3ex] 0.3m + 55; \hspace{2.5em} 400 \lt m \le 800 \\[3ex] 295; \hspace{5.5em} 800 \lt m \le 960 \end{cases} $

−4 lies in the domain for the first piece
0 is in the domain of the second piece
4 is in the domain of the third piece

$ (a.) \\[3ex] f(x) = x^2 \\[3ex] f(-4) = (-4)^2 \\[3ex] f(-4) = 16 \\[3ex] (b.) \\[3ex] f(x) = -2 \\[3ex] f(0) = -2 \\[3ex] (c.) \\[3ex] f(x) = 3x + 4 \\[3ex] f(4) = 3(4) + 4 \\[3ex] f(4) = 12 + 4 \\[3ex] f(4) = 16 $

(a.) t = 5°C
v = 0.5 m/sec
0.5 < 0.78
Therefore, the domain falls in the first piece
W = t = 5°C

(b.) t = 5°C
v = 19 m/sec
1.78 ≤ 19 ≤ 25
Therefore, the domain falls in the second piece

$ W = 33 - \dfrac{(10.43 + 10\sqrt{v} - v)(33 - t)}{22.04} \\[5ex] = 33 - \dfrac{(10.43 + 10\sqrt{19} - 19)(33 - 5)}{22.04} \\[5ex] = 33 - \dfrac{(10.43 + 10(4.358898944) - 19)(33 - 5)}{22.04} \\[5ex] = 33 - \dfrac{(10.43 + 43.58898944 - 19)(28)}{22.04} \\[5ex] = 33 - \dfrac{(10.43 + 43.58898944 - 19)(28)}{22.04} \\[5ex] = 33 - \dfrac{28(35.01898944)}{22.04} \\[5ex] = 33 - \dfrac{980.5317042}{22.04} \\[5ex] = 33 - 44.48873431 \\[3ex] = -11.48873431 \\[3ex] \approx -11^\circ \\[3ex] $ (c.) t = 5°C
v = 32 m/sec
32 > 25
Therefore, the domain falls in the third piece

$ W = 33 - 1.5957(33 - t) \\[3ex] W = 33 - 1.5957(33 - 5) \\[3ex] = 33 - 1.5957(28) \\[3ex] = 33 - 44.6796 \\[3ex] = -11.6796 \\[3ex] \approx -12^\circ $

0 lies in the domain for the first piece
1 lies in the domain for the first piece
5 lies in the domain for the first piece
6 lies in the domain for the second piece

$ (a.) \\[3ex] f(x) = 3x - 5 \\[3ex] f(0) = 3(0) - 5 \\[3ex] f(0) = 0 - 5 \\[3ex] f(0) = -5 \\[3ex] (b.) \\[3ex] f(1) = 3(1) - 5 \\[3ex] f(1) = 3 - 5 \\[3ex] f(1) = -2 \\[3ex] (c.) \\[3ex] f(5) = 3(5) - 5 \\[3ex] f(5) = 15 - 5 \\[3ex] f(5) = 10 \\[3ex] (d.) \\[3ex] f(x) = x^3 - 5 \\[3ex] f(6) = 6^3 - 5 \\[3ex] f(6) = 216 - 5 \\[3ex] f(6) = 211 $

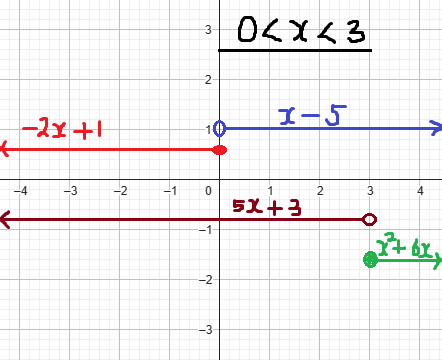
1st Step
Compare domains: domain of 1st piece of $f(x)$ and domain of 1st piece of $g(x)$
x < 1 and x ≤ 0
x ≤ 0 also includes x < 1
∴ x ≤ 0 becomes the first domain of the sum function

2nd Step
Determine the sum function for the first domain (1st piece)
$ (f + g)(x) \\[3ex] = f(x) + g(x) \\[3ex] = (3x + 7) + (-5x + 1) \\[3ex] = 3x + 7 - 5x + 1 \\[3ex] = -2x + 8 \\[3ex] $ 3rd Step
Compare domains: domain of 1st piece of $f(x)$ and domain of 2nd piece of $g(x)$
x < 1 and x > 0
⇒ x < 1 and 0 < x
⇒ 0 < x < 1
This becomes the second domain of the sum function

4th Step
Determine the sum function for the second domain (2nd piece)
$ (f + g)(x) \\[3ex] = f(x) + g(x) \\[3ex] = (3x + 7) + (x - 8) \\[3ex] = 3x + 7 + x - 8 \\[3ex] = 4x - 1 \\[3ex] $ 5th Step
Compare domains: domain of 2nd piece of $f(x)$ and domain of 2nd piece of $g(x)$
x ≥ 1 and x > 0
x ≥ 1 also includes x > 0
∴ x ≥ 1 becomes the third domain of the sum function

6th Step
Determine the sum function for the third domain (3rd piece)
$ (f + g)(x) \\[3ex] = f(x) + g(x) \\[3ex] = (x^2 + 3x) + (x - 8) \\[3ex] = x^2 + 3x + x - 8 \\[3ex] = x^2 + 4x - 8 \\[3ex] $ The Piecewise Function of the Sum Function is:

$ (f + g)(x) = \begin{cases} -2x + 8; \hspace{3.7em} x \le 0 \\[3ex] 4x - 1; \hspace{4.3em} 0 \lt x \lt 1 \\[3ex] x^2 + 4x - 8; \hspace{2em} x \ge 1 \end{cases} $

$ f(x) = int(2x) \\[3ex] (a.) \\[3ex] f(3.3) = int[2(3.3)] \\[3ex] = int(6.6) \\[3ex] = 6 \\[3ex] (b.) \\[3ex] f(-2.6) = int[2(-2.6)] \\[3ex] = int(-5.2) \\[3ex] = -6 \\[3ex] (c.) \\[3ex] f(3.9) = int[2(3.9)] \\[3ex] = int(7.8) \\[3ex] = 7 $

$ 11\% = \dfrac{11}{100} = 0.11 \\[5ex] 16\% = \dfrac{16}{100} = 0.16 \\[5ex] 24\% = \dfrac{24}{100} = 0.24 \\[5ex] 33\% = \dfrac{33}{100} = 0.33 \\[5ex] f(x) = \begin{cases} 0.11x \hspace{82mm} \text{if} \hspace{5mm} 0 \lt x \le 7,550 \\[3ex] 830.5 + 0.16(x - 7550) \hspace{31mm} \text{if} \hspace{5mm} 7,500 \lt x \le 30,700 \\[3ex] 4534.5 + 0.24(x - 30700) \hspace{24mm} \text{if} \hspace{5mm} 30,700 \lt x \le 74,300 \\[3ex] 14,998.5 + 0.33(x - 74300) \hspace{18mm} \text{if} \hspace{5mm} x \gt 74,300 \end{cases} $

$ At\;\;y-intercept;\;\; x = 0 \\[3ex] This\;\;falls\;\;in\;\;the\;\;second\;\;piece \\[3ex] f(x) = 2x - 5 \\[3ex] f(0) = 2(0) - 5 \\[3ex] f(0) = 0 - 5 \\[3ex] f(0) = -5 $

(a.) 150 is in the domain of the first piece.

$ C(150) = \$34.99 \\[3ex] $ (b.) 330 is in the domain of the second piece.

$ C(330) = 0.25(330) - 40.01 \\[3ex] = 82.5 - 40.01 \\[3ex] = \$42.49 \\[3ex] $ (c.) 301 is in the domain of the second piece.

$ C(301) = 0.25(301) - 40.01 \\[3ex] = 72.25 - 40.01 \\[3ex] = \$35.24 $

Let us review a visual representation of these functions.



1st Step
Compare domains: domain of 1st piece of $f(x)$ and domain of 1st piece of $g(x)$
x < 3 and x ≤ 0
x ≤ 0 also includes x < 3
∴ x ≤ 0 becomes the first domain of the sum function

2nd Step
Determine the sum function for the first domain (1st piece)
$ (f + g)(x) \\[3ex] = f(x) + g(x) \\[3ex] = (5x + 3) + (-2x + 1) \\[3ex] = 5x + 3 - 2x + 1 \\[3ex] = 3x + 4 \\[3ex] $ 3rd Step
Compare domains: domain of 1st piece of $f(x)$ and domain of 2nd piece of $g(x)$
x < 3 and x > 0
⇒ x < 3 and 0 < x
⇒ 0 < x < 3
This becomes the second domain of the sum function

4th Step
Determine the sum function for the second domain (2nd piece)
$ (f + g)(x) \\[3ex] = f(x) + g(x) \\[3ex] = (5x + 3) + (x - 5) \\[3ex] = 5x + 3 + x - 5 \\[3ex] = 6x - 2 \\[3ex] $ 5th Step
Compare domains: domain of 2nd piece of $f(x)$ and domain of 2nd piece of $g(x)$
x ≥ 3 and x > 0
x ≥ 3 also includes x > 0
∴ x ≥ 3 becomes the third domain of the sum function

6th Step
Determine the sum function for the third domain (3rd piece)
$ (f + g)(x) \\[3ex] = f(x) + g(x) \\[3ex] = (x^2 + 6x) + (x - 5) \\[3ex] = x^2 + 6x + x - 5 \\[3ex] = x^2 + 7x - 5 \\[3ex] $ The Piecewise Function of the Sum Function is:

$ (f + g)(x) = \begin{cases} 3x + 4; \hspace{3.9em} x \le 0 \\[3ex] 6x - 2; \hspace{4.1em} 0 \lt x \lt 3 \\[3ex] x^2 + 7x - 5; \hspace{2em} x \ge 3 \end{cases} $

$ 3.75\% = \dfrac{3.75}{100} = 0.0375 \\[5ex] 0.0375(400000) = 15000 \\[3ex] 2.5\% = \dfrac{2.5}{100} = 0.025 \\[5ex] 0.025(400000) = 10000 \\[3ex] 1.5\% = \dfrac{1.5}{100} = 0.015 \\[5ex] 0.015(400000) = 6000 \\[3ex] 1\% = \dfrac{1}{100} = 0.01 \\[5ex] 0.01(400000) = 4000 \\[3ex] 0.75\% = \dfrac{0.75}{100} = 0.0075 \\[5ex] 0.0075(400000) = 3000 \\[3ex] 0.25\% = \dfrac{0.25}{100} = 0.0025 \\[5ex] 0.0025(400000) = 1000 \\[3ex] (a.) \\[3ex] C(s) = \begin{cases} \$15000 \hspace{21mm} \text{if} \hspace{5mm} s \le 659 \\[3ex] \$10000 \hspace{21mm} \text{if} \hspace{5mm} 660 \le s \le 679 \\[3ex] \$6000 \hspace{25mm} \text{if} \hspace{5mm} 680 \le s \le 699 \\[3ex] \$4000 \hspace{25mm} \text{if} \hspace{5mm} 700 \le s \le 719 \\[3ex] \$3000 \hspace{25mm} \text{if} \hspace{5mm} 720 \le s \le 739 \\[3ex] \$1000 \hspace{25mm} \text{if} \hspace{5mm} s \ge 740 \\[3ex] \end{cases} \\[10ex] (b.) \\[3ex] C(712) = \$4000 \\[3ex] (c.) \\[3ex] C(684) = \$6000 $

(a.) −4 is not in any domain.
Therefore, f(−4) has no value.

(b.) 4 is in the domain of the third piece.
f(4) = −4 + 5
f(4) = 1

(c.) 3.5 is in the domain of the third piece.
f(3.5) = −3.5 + 5
f(3.5) = 1.5

(d.) 1 is in the domain of the second piece.
f(1) = 4

(e.) To find the domain, let us look at the domain of the first and third pieces.
The domain of the second piece has values that are already included.
So, we shall focus only on the domains of the first and third pieces because it will help us determine the first endpoint and the third endpoint of the domain respectively.
The domain of the first piece begins with −3 as the first included endpoint.
The domain of the third piece ends with positive infinity.
D = [−3, ∞)

(f.) To find the range, let us find the beginning and end values of the function in each piece.
For the last piece, we shall find intermediate values because it has no end value.
For the last piece, we need to find several interdiate values so we can see the pattern of the values: increasing, decreasing, or constant values.

$ \underline{1st\;\;Piece} \\[3ex] Function:\;\; f(x) = -x^2 + 4 \\[3ex] Domain:\;\; -3 \le x \lt 0 \\[3ex] Beginning\;\;value:\;\; f(-3) = -(-3)^2 + 4 \\[3ex] = -9 + 4 \\[3ex] = -5\;(included) \\[3ex] Ending\;\;value:\;\; f(0) = -(0)^2 + 4 \\[3ex] = -0 + 4 \\[3ex] = 4\;(excluded) \\[3ex] All\;\;values\;\;from\;\;-5\;(included)\;\;to\;\;4\;(excluded)\;\;are\;\;included. \\[5ex] \underline{2nd\;\;Piece} \\[3ex] Function:\;\; f(x) = 4 \\[3ex] Domain:\;\; 0 \le x \lt 3 \\[3ex] Beginning\;\;value:\;\; f(0) = 4\;(included) \\[3ex] Ending\;\;value:\;\; f(3) = 4\;(excluded) \\[3ex] 4\;\;is\;\;included. \\[5ex] \underline{3rd\;\;Piece} \\[3ex] Function:\;\; f(x) = -x + 5 \\[3ex] Domain:\;\; x \ge 3 \\[3ex] Beginning\;\;value:\;\; f(3) = -3 + 5 = 2\;(included) \\[3ex] Intermediate\;\;values\;(included): \\[3ex] f(4) = -4 + 5 = 1 \\[3ex] f(5) = -5 + 5 = 0 \\[3ex] f(6) = -6 + 5 = -1 \\[3ex] f(7) = -7 + 5 = -2 \\[3ex] f(8) = -8 + 5 = -3 \\[3ex] ...decreasing\;\;pattern\;\;up\;\;to\;\;negative\;\;infinity\;(excluded) \\[3ex] From\;\;2\;(included)\;\;to\;\;-\infty\;(excluded)\;\;are\;\;included. \\[5ex] \underline{Entire:\;\;Piecewise\;\;Function} \\[3ex] Highest\;\;negative\;\;value = -\infty \\[3ex] Highest\;\;positive\;\;value = 4 \\[3ex] \therefore R = (-\infty, 4] \\[3ex] $ (g.) What interval of x does the value of y increase?
The value of y increases in the first domain: from −5 through 4
The interval on which this occurs is from −3 to 0

$ f(x) \uparrow x \in (-3, 0) \\[3ex] $ (h.) What interval of x does the value of y decrease?
The value of y decreases in the third domain: from negative infinity to 4
The interval on which this occurs is from 3 to infinity

$ f(x) \downarrow x \in (3, \infty) \\[3ex] $ (i.) What interval of x is the value of y a constant?
The value of y is constant in the second domain: 4
The interval on which this occurs is from 0 to 3

$ f(x) \rightarrow x \in (0, 3) \\[3ex] $